Horizon cosmologique

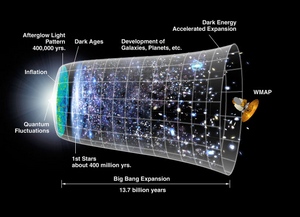
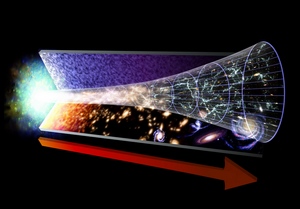
Dans les modèles de Big Bang, le temps est limité dans le passé. L'univers qui nous est observable se compose des objets qui nous ont envoyé de la lumière qui, entre t = 0 et t = t0, a eu le temps de nous parvenir. C'est ce qu'on appelle l'horizon. Pour un objet proche, la lumière qui nous parvient au bout d'un temps t a voyagé sur une distance de ct, qui est donc la distance de l'objet. Mais pour un objet très lointain, les choses sont extrêmement différentes. Prenons l'exemple (tiré de Seguin & Villeneuve, Masson ed.) d'une galaxie située à 3,5 10⁹ années lumière de nous à l'instant t0 - 9.10⁹ ans, c'est à dire il y a 9 milliards d'années. On peut montrer que le photon parti de cette galaxie dans notre direction, se déplaçant vers nous à la vitesse c dans un espace en expansion qui contrarie son mouvement (on suppose ici H0 = 65 km s^-1 Mpc^-1) nous parviendra dans 9 milliards d'années, alors qu'il est parti d'un objet qui était à 3,5 milliards d'années lumière seulement; et que quand nous le recevrons, la galaxie qui aura continué son chemin se trouvera alors à 15,8 milliards d'années lumière de nous. On voit donc tel qu'il était il y a 9 milliards d'années, quand il était à 3,5 milliards d'années lumière de nous, un objet qui se trouve à 15,8 milliards d'années lumière... Pas simple !

Alors, quel est le rayon de l'univers observable à un instant donné ? On peut montrer qu'il est à peu près égal, exprimé en années-lumière, à trois fois l'âge de l'univers exprimé en années.

Ce rayon croît donc avec le temps, mais il existe une limite absolue : quand on observe des objets de plus en plus lointains, on remonte dans le passé. Mais on ne pourra jamais voir au-delà de l'époque de la recombinaison, puisqu'auparavant l'univers ne permettait pas la circulation de la lumière, n'était pas transparent. Cette époque, nous l'avons vu correspond à t = 300 000 à 1 000 000 d'années. On parle à son propos de brume cosmologique.